In my previous blog about a Survival Analysis of the NASA C-MAPSS turbofan jet engine data set, we also tried to use its methods for the purpose of predictive maintenance of jet engines eventually with only limited success.
Therefore I’d like to find and set up a more performant (reliable) solution in detecting degradation in the engines conditions through the sensor measurement data by means of binary classification of time series windows. That data will have to be labeled appropiately. I want to avoid any False Negative classification instances as I assume the cost related to an engine failure in the field to be multiple times higher than False Positive instances, in which case engines just get maintenanced/replaced relatively too early.
import os
os.environ['TF_CUDNN_DETERMINISTIC']='1'
import tensorflow as tf
print(tf.__version__)
2.5.0
print(f"Tensorflow version: {tf.__version__}")
print(f"Keras Version: {tf.keras.__version__}")
print("GPU is", "available" if tf.config.list_physical_devices('GPU') else "NOT AVAILABLE")
Tensorflow version: 2.5.0
Keras Version: 2.5.0
GPU is available
!python --version
Python 3.8.11
print('\n'.join(f'{m.__name__}=={m.__version__}' for m in globals().values() if getattr(m, '__version__', None)))
tensorflow==2.5.0
pandas==1.2.4
numpy==1.19.5
seaborn==0.11.2
import sys
print('current env:' , sys.exec_prefix.split(os.sep)[-1] )
current env: tf25
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('darkgrid')
from numpy.random import RandomState, SeedSequence, MT19937
seed=1
rng = RandomState(MT19937(SeedSequence(seed)))
from sklearn import preprocessing
#from sklearn.metrics import confusion_matrix, recall_score, precision_score, f1_score
model_path = 'clf_model.h5'
columnnames = ['id', 'cycle', 'setting1', 'setting2', 'setting3', 's1', 's2', 's3',
's4', 's5', 's6', 's7', 's8', 's9', 's10', 's11', 's12', 's13', 's14',
's15', 's16', 's17', 's18', 's19', 's20', 's21']
train_df = pd.read_csv('CMaps/train_FD002.txt', sep=" ", header=None)
train_df = train_df.drop(train_df.columns[[26, 27]], axis=1)
train_df.columns = columnnames
train_df = train_df.sort_values(['id','cycle'])
test_df = pd.read_csv('CMaps/test_FD002.txt', sep=" ", header=None)
test_df = test_df.drop(test_df.columns[[26, 27]], axis=1)
test_df.columns = columnnames
# read RUL labels = vector of true Remaining Useful Life (RUL) values for the test data
test_RUL_df = pd.read_csv('CMaps/RUL_FD002.txt', sep=" ", header=None)
test_RUL_df = test_RUL_df.drop(test_RUL_df.columns[[1]], axis=1)
testmachineids = test_df.id.unique()
len(test_df.id.unique())
259
Data Preprocessing
Training Data
# Data Labeling - generate column RUL(Remaining Usefull Life or Time to Failure)
rul = pd.DataFrame(train_df.groupby('id')['cycle'].max()).reset_index()
rul.columns = ['id', 'max']
train_df = train_df.merge(rul, on=['id'], how='left')
train_df['RUL'] = train_df['max'] - train_df['cycle']
train_df.drop('max', axis=1, inplace=True)
# generate label columns for training data
# is a failure state imminent?
w1 = 30
w0 = 15
train_df['label1'] = np.where(train_df['RUL'] <= w1, 1, 0 )
train_df['label2'] = train_df['label1']
train_df.loc[train_df['RUL'] <= w0, 'label2'] = 2
# MinMax normalization (from 0 to 1)
cols_normalize = train_df.columns.difference(['id','cycle','RUL','label1','label2'])
min_max_scaler = preprocessing.MinMaxScaler()
norm_train_df = pd.DataFrame(min_max_scaler.fit_transform(train_df[cols_normalize]),
columns=cols_normalize,
index=train_df.index)
join_df = train_df[train_df.columns.difference(cols_normalize)].join(norm_train_df)
train_df = join_df.reindex(columns = train_df.columns)
train_df
| id | cycle | setting1 | setting2 | setting3 | s1 | s2 | s3 | s4 | s5 | ... | s15 | s16 | s17 | s18 | s19 | s20 | s21 | RUL | label1 | label2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0.833134 | 0.997625 | 1.0 | 0.060269 | 0.181576 | 0.311201 | 0.273095 | 0.146592 | ... | 0.369947 | 0.0 | 0.322917 | 0.651163 | 1.0 | 0.156036 | 0.159082 | 148 | 0 | 0 |
| 1 | 1 | 2 | 0.999767 | 0.998575 | 1.0 | 0.000000 | 0.131847 | 0.296600 | 0.245535 | 0.000000 | ... | 0.381407 | 0.0 | 0.281250 | 0.627907 | 1.0 | 0.007888 | 0.014562 | 147 | 0 | 0 |
| 2 | 1 | 3 | 0.595096 | 0.738480 | 0.0 | 0.238089 | 0.016332 | 0.035297 | 0.056997 | 0.293184 | ... | 0.936731 | 0.0 | 0.062500 | 0.000000 | 0.0 | 0.133745 | 0.151414 | 146 | 0 | 0 |
| 3 | 1 | 4 | 0.999993 | 0.999525 | 1.0 | 0.000000 | 0.128269 | 0.298795 | 0.246979 | 0.000000 | ... | 0.372400 | 0.0 | 0.270833 | 0.627907 | 1.0 | 0.014060 | 0.026144 | 145 | 0 | 0 |
| 4 | 1 | 5 | 0.595137 | 0.736698 | 0.0 | 0.238089 | 0.014130 | 0.037871 | 0.058152 | 0.293184 | ... | 0.937537 | 0.0 | 0.062500 | 0.000000 | 0.0 | 0.135460 | 0.143240 | 144 | 0 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 53754 | 260 | 312 | 0.476188 | 0.831354 | 1.0 | 0.626985 | 0.672172 | 0.682297 | 0.591489 | 0.507937 | ... | 0.354350 | 1.0 | 0.687500 | 0.864693 | 1.0 | 0.486283 | 0.483993 | 4 | 1 | 2 |
| 53755 | 260 | 313 | 0.238102 | 0.298100 | 1.0 | 0.597937 | 0.644830 | 0.733008 | 0.722934 | 0.617180 | ... | 0.154840 | 1.0 | 0.739583 | 0.854123 | 1.0 | 0.614540 | 0.622022 | 3 | 1 | 2 |
| 53756 | 260 | 314 | 0.595222 | 0.736342 | 0.0 | 0.238089 | 0.017892 | 0.088067 | 0.082198 | 0.293184 | ... | 0.999561 | 0.0 | 0.072917 | 0.000000 | 0.0 | 0.137517 | 0.144474 | 2 | 1 | 2 |
| 53757 | 260 | 315 | 0.595203 | 0.738717 | 0.0 | 0.238089 | 0.021195 | 0.079155 | 0.102368 | 0.293184 | ... | 0.995167 | 0.0 | 0.083333 | 0.000000 | 0.0 | 0.132716 | 0.134383 | 1 | 1 | 2 |
| 53758 | 260 | 316 | 0.833260 | 0.997625 | 1.0 | 0.060269 | 0.193687 | 0.354544 | 0.293049 | 0.146592 | ... | 0.389609 | 0.0 | 0.364583 | 0.651163 | 1.0 | 0.156722 | 0.161215 | 0 | 1 | 2 |
53759 rows × 29 columns
Testing Data
# MinMax normalization (from 0 to 1)
norm_test_df = pd.DataFrame(min_max_scaler.transform(test_df[cols_normalize]),
columns=cols_normalize,
index=test_df.index)
test_join_df = test_df[test_df.columns.difference(cols_normalize)].join(norm_test_df)
test_df = test_join_df.reindex(columns = test_df.columns)
test_df = test_df.reset_index(drop=True)
# most current cycle till observation time point
test_currentcycle = pd.DataFrame(test_df.groupby('id')['cycle'].max()).reset_index()
test_currentcycle.columns = ['id', 'max']
# test data RUL
test_RUL_df.columns = ['remaining_RUL_at_obs']
test_RUL_df['id'] = test_RUL_df.index + 1
# absolute max lifetime duration in cycles (RUL at cycle 0)
test_RUL_df['max'] = test_currentcycle['max'] + test_RUL_df['remaining_RUL_at_obs']
test_RUL_df.drop('remaining_RUL_at_obs', axis=1, inplace=True)
# generate RUL for test data
test_df = test_df.merge(test_RUL_df, on=['id'], how='left')
test_df['RUL'] = test_df['max'] - test_df['cycle']
test_df.drop('max', axis=1, inplace=True)
# generate labels for imminent failure indication
test_df['label1'] = np.where(test_df['RUL'] <= w1, 1, 0 )
test_df['label2'] = test_df['label1']
test_df.loc[test_df['RUL'] <= w0, 'label2'] = 2
#test_RUL_df
Prepare time series data as time window arrays
# window cycle duration
window_width = 30
# function to reshape features into (samples, time steps, features)
def gen_time_windows(id_df, window_width, scols):
""" Create time series time windows arrays for training """
# for one id I put all the rows in a single matrix
data_matrix = id_df[scols].values
num_elements = data_matrix.shape[0]
for start, stop in zip(range(0, num_elements-window_width), range(window_width, num_elements)):
yield data_matrix[start:stop, :]
scols = ['s' + str(i) for i in range(1,22)] + ['setting1', 'setting2', 'setting3',
#'cycle_norm'
]
# generator for the windows
win_gen = (list(gen_time_windows(train_df[train_df['id']==id], window_width, scols))
for id in train_df['id'].unique())
# generate sequences and convert to numpy array
seq_array = np.concatenate(list(win_gen)).astype(np.float32)
seq_array.shape
# label func
def gen_labels(id_df, window_width, label):
data_matrix = id_df[label].values
num_elements = data_matrix.shape[0]
return data_matrix[window_width:num_elements, :]
# generate labels
label_gen = [gen_labels(train_df[train_df['id']==id], window_width, ['label1'])
for id in train_df['id'].unique()]
label_array = np.concatenate(label_gen).astype(np.float32)
nb_features = seq_array.shape[2]
nb_out = label_array.shape[1]
seq_array.shape
nb_out
1
len(label_array)
45959
Recurrent Neural Network (RNN) as Gated Recurrent Units (GRU)
try:
model
except NameError:
print("session was clear already")
else:
tf.keras.backend.clear_session()
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.GRU(
input_shape=(window_width, nb_features),
units=100,
return_sequences=True))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.GRU(
units=50,
return_sequences=False))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(units=nb_out, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam',
metrics=tf.keras.metrics.Recall()
)
print(model.summary())
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru (GRU) (None, 30, 100) 37800
_________________________________________________________________
dropout (Dropout) (None, 30, 100) 0
_________________________________________________________________
gru_1 (GRU) (None, 50) 22800
_________________________________________________________________
dropout_1 (Dropout) (None, 50) 0
_________________________________________________________________
dense (Dense) (None, 1) 51
=================================================================
Total params: 60,651
Trainable params: 60,651
Non-trainable params: 0
_________________________________________________________________
None
%%time
# fit the network
history = model.fit(seq_array, label_array, epochs=120, batch_size=200, validation_split=0.1, verbose=2,
callbacks = [tf.keras.callbacks.EarlyStopping( monitor='recall',
min_delta=0, patience=20, verbose=0, mode='max'),
tf.keras.callbacks.ModelCheckpoint(model_path,
monitor='val_recall',
save_best_only=True, mode='max', verbose=0)
]
)
# list all data in history
print(history.history.keys())
Epoch 1/120
207/207 - 2s - loss: 0.1143 - recall: 0.8486 - val_loss: 0.1311 - val_recall: 0.8852
Epoch 2/120
207/207 - 2s - loss: 0.0983 - recall: 0.8733 - val_loss: 0.1475 - val_recall: 0.9110
Epoch 3/120
207/207 - 2s - loss: 0.0962 - recall: 0.8755 - val_loss: 0.1547 - val_recall: 0.9032
Epoch 4/120
207/207 - 2s - loss: 0.0925 - recall: 0.8861 - val_loss: 0.1726 - val_recall: 0.8348
Epoch 5/120
207/207 - 2s - loss: 0.0805 - recall: 0.8987 - val_loss: 0.1969 - val_recall: 0.9303
Epoch 6/120
207/207 - 2s - loss: 0.0743 - recall: 0.9068 - val_loss: 0.1648 - val_recall: 0.8490
Epoch 7/120
207/207 - 2s - loss: 0.0729 - recall: 0.9112 - val_loss: 0.1693 - val_recall: 0.8116
Epoch 8/120
207/207 - 2s - loss: 0.0656 - recall: 0.9211 - val_loss: 0.2027 - val_recall: 0.9045
Epoch 9/120
207/207 - 2s - loss: 0.0659 - recall: 0.9207 - val_loss: 0.1823 - val_recall: 0.7432
Epoch 10/120
207/207 - 2s - loss: 0.0535 - recall: 0.9359 - val_loss: 0.2170 - val_recall: 0.8142
Epoch 11/120
207/207 - 2s - loss: 0.0465 - recall: 0.9434 - val_loss: 0.2457 - val_recall: 0.7948
Epoch 12/120
207/207 - 2s - loss: 0.0456 - recall: 0.9448 - val_loss: 0.2920 - val_recall: 0.8490
Epoch 13/120
207/207 - 2s - loss: 0.0423 - recall: 0.9482 - val_loss: 0.2724 - val_recall: 0.7432
Epoch 14/120
207/207 - 2s - loss: 0.0329 - recall: 0.9595 - val_loss: 0.2958 - val_recall: 0.8606
Epoch 15/120
207/207 - 2s - loss: 0.0292 - recall: 0.9655 - val_loss: 0.3193 - val_recall: 0.8619
Epoch 16/120
207/207 - 2s - loss: 0.0375 - recall: 0.9563 - val_loss: 0.2482 - val_recall: 0.7032
Epoch 17/120
207/207 - 2s - loss: 0.0337 - recall: 0.9576 - val_loss: 0.3247 - val_recall: 0.8452
Epoch 18/120
207/207 - 2s - loss: 0.0248 - recall: 0.9716 - val_loss: 0.2981 - val_recall: 0.7858
Epoch 19/120
207/207 - 2s - loss: 0.0303 - recall: 0.9639 - val_loss: 0.3764 - val_recall: 0.9135
Epoch 20/120
207/207 - 2s - loss: 0.0233 - recall: 0.9719 - val_loss: 0.3826 - val_recall: 0.8542
Epoch 21/120
207/207 - 2s - loss: 0.0212 - recall: 0.9758 - val_loss: 0.3639 - val_recall: 0.8103
Epoch 22/120
207/207 - 2s - loss: 0.0206 - recall: 0.9746 - val_loss: 0.3655 - val_recall: 0.7587
Epoch 23/120
207/207 - 2s - loss: 0.0201 - recall: 0.9769 - val_loss: 0.4157 - val_recall: 0.8490
Epoch 24/120
207/207 - 2s - loss: 0.0220 - recall: 0.9741 - val_loss: 0.4530 - val_recall: 0.8503
Epoch 25/120
207/207 - 2s - loss: 0.0234 - recall: 0.9720 - val_loss: 0.3770 - val_recall: 0.8426
Epoch 26/120
207/207 - 2s - loss: 0.0202 - recall: 0.9750 - val_loss: 0.3363 - val_recall: 0.8503
Epoch 27/120
207/207 - 2s - loss: 0.0223 - recall: 0.9749 - val_loss: 0.4185 - val_recall: 0.7819
Epoch 28/120
207/207 - 2s - loss: 0.0178 - recall: 0.9794 - val_loss: 0.3179 - val_recall: 0.7974
Epoch 29/120
207/207 - 2s - loss: 0.0198 - recall: 0.9747 - val_loss: 0.3727 - val_recall: 0.7742
Epoch 30/120
207/207 - 2s - loss: 0.0169 - recall: 0.9813 - val_loss: 0.5387 - val_recall: 0.9071
Epoch 31/120
207/207 - 2s - loss: 0.0129 - recall: 0.9837 - val_loss: 0.3979 - val_recall: 0.7987
Epoch 32/120
207/207 - 2s - loss: 0.0179 - recall: 0.9801 - val_loss: 0.4818 - val_recall: 0.8516
Epoch 33/120
207/207 - 2s - loss: 0.0127 - recall: 0.9852 - val_loss: 0.3982 - val_recall: 0.7987
Epoch 34/120
207/207 - 2s - loss: 0.0241 - recall: 0.9723 - val_loss: 0.4336 - val_recall: 0.8206
Epoch 35/120
207/207 - 2s - loss: 0.0134 - recall: 0.9849 - val_loss: 0.4261 - val_recall: 0.7587
Epoch 36/120
207/207 - 2s - loss: 0.0105 - recall: 0.9881 - val_loss: 0.4880 - val_recall: 0.8361
Epoch 37/120
207/207 - 2s - loss: 0.0139 - recall: 0.9838 - val_loss: 0.5099 - val_recall: 0.8335
Epoch 38/120
207/207 - 2s - loss: 0.0140 - recall: 0.9834 - val_loss: 0.4014 - val_recall: 0.7665
Epoch 39/120
207/207 - 2s - loss: 0.0165 - recall: 0.9813 - val_loss: 0.4473 - val_recall: 0.8245
Epoch 40/120
207/207 - 2s - loss: 0.0098 - recall: 0.9882 - val_loss: 0.5178 - val_recall: 0.7794
Epoch 41/120
207/207 - 2s - loss: 0.0126 - recall: 0.9868 - val_loss: 0.4789 - val_recall: 0.6710
Epoch 42/120
207/207 - 2s - loss: 0.0177 - recall: 0.9805 - val_loss: 0.3225 - val_recall: 0.8194
Epoch 43/120
207/207 - 2s - loss: 0.0102 - recall: 0.9882 - val_loss: 0.6370 - val_recall: 0.8929
Epoch 44/120
207/207 - 2s - loss: 0.0116 - recall: 0.9879 - val_loss: 0.4765 - val_recall: 0.7561
Epoch 45/120
207/207 - 2s - loss: 0.0124 - recall: 0.9860 - val_loss: 0.4893 - val_recall: 0.8594
Epoch 46/120
207/207 - 2s - loss: 0.0114 - recall: 0.9878 - val_loss: 0.4624 - val_recall: 0.8013
Epoch 47/120
207/207 - 2s - loss: 0.0107 - recall: 0.9889 - val_loss: 0.4311 - val_recall: 0.7729
Epoch 48/120
207/207 - 2s - loss: 0.0088 - recall: 0.9900 - val_loss: 0.5615 - val_recall: 0.8439
Epoch 49/120
207/207 - 2s - loss: 0.0158 - recall: 0.9831 - val_loss: 0.4089 - val_recall: 0.8168
Epoch 50/120
207/207 - 2s - loss: 0.0077 - recall: 0.9920 - val_loss: 0.4983 - val_recall: 0.8361
Epoch 51/120
207/207 - 2s - loss: 0.0060 - recall: 0.9926 - val_loss: 0.5005 - val_recall: 0.7523
Epoch 52/120
207/207 - 2s - loss: 0.0152 - recall: 0.9827 - val_loss: 0.5162 - val_recall: 0.8581
Epoch 53/120
207/207 - 2s - loss: 0.0072 - recall: 0.9922 - val_loss: 0.5679 - val_recall: 0.8310
Epoch 54/120
207/207 - 2s - loss: 0.0090 - recall: 0.9898 - val_loss: 0.4661 - val_recall: 0.7471
Epoch 55/120
207/207 - 2s - loss: 0.0087 - recall: 0.9912 - val_loss: 0.5827 - val_recall: 0.5277
Epoch 56/120
207/207 - 2s - loss: 0.0095 - recall: 0.9889 - val_loss: 0.5227 - val_recall: 0.7613
Epoch 57/120
207/207 - 2s - loss: 0.0078 - recall: 0.9908 - val_loss: 0.6695 - val_recall: 0.8374
Epoch 58/120
207/207 - 2s - loss: 0.0083 - recall: 0.9907 - val_loss: 0.6034 - val_recall: 0.8168
Epoch 59/120
207/207 - 2s - loss: 0.0064 - recall: 0.9929 - val_loss: 0.5060 - val_recall: 0.8387
Epoch 60/120
207/207 - 2s - loss: 0.0296 - recall: 0.9709 - val_loss: 0.4557 - val_recall: 0.7200
Epoch 61/120
207/207 - 2s - loss: 0.0054 - recall: 0.9957 - val_loss: 0.5439 - val_recall: 0.8077
Epoch 62/120
207/207 - 2s - loss: 0.0061 - recall: 0.9938 - val_loss: 0.4883 - val_recall: 0.7948
Epoch 63/120
207/207 - 2s - loss: 0.0076 - recall: 0.9911 - val_loss: 0.5010 - val_recall: 0.8206
Epoch 64/120
207/207 - 2s - loss: 0.0044 - recall: 0.9953 - val_loss: 0.5414 - val_recall: 0.7032
Epoch 65/120
207/207 - 2s - loss: 0.0097 - recall: 0.9883 - val_loss: 0.5510 - val_recall: 0.8671
Epoch 66/120
207/207 - 2s - loss: 0.0069 - recall: 0.9922 - val_loss: 0.4558 - val_recall: 0.7368
Epoch 67/120
207/207 - 2s - loss: 0.0142 - recall: 0.9867 - val_loss: 0.4797 - val_recall: 0.8000
Epoch 68/120
207/207 - 2s - loss: 0.0040 - recall: 0.9964 - val_loss: 0.5577 - val_recall: 0.8039
Epoch 69/120
207/207 - 2s - loss: 0.0060 - recall: 0.9938 - val_loss: 0.5344 - val_recall: 0.7290
Epoch 70/120
207/207 - 2s - loss: 0.0054 - recall: 0.9938 - val_loss: 0.5678 - val_recall: 0.8581
Epoch 71/120
207/207 - 2s - loss: 0.0072 - recall: 0.9929 - val_loss: 0.5642 - val_recall: 0.8387
Epoch 72/120
207/207 - 2s - loss: 0.0068 - recall: 0.9929 - val_loss: 0.5317 - val_recall: 0.5897
Epoch 73/120
207/207 - 2s - loss: 0.0056 - recall: 0.9938 - val_loss: 0.5957 - val_recall: 0.7458
Epoch 74/120
207/207 - 2s - loss: 0.0050 - recall: 0.9949 - val_loss: 0.5478 - val_recall: 0.6839
Epoch 75/120
207/207 - 2s - loss: 0.0114 - recall: 0.9882 - val_loss: 0.5366 - val_recall: 0.6581
Epoch 76/120
207/207 - 2s - loss: 0.0049 - recall: 0.9946 - val_loss: 0.5548 - val_recall: 0.7187
Epoch 77/120
207/207 - 2s - loss: 0.0053 - recall: 0.9942 - val_loss: 0.5235 - val_recall: 0.7871
Epoch 78/120
207/207 - 2s - loss: 0.0050 - recall: 0.9951 - val_loss: 0.5876 - val_recall: 0.6155
Epoch 79/120
207/207 - 2s - loss: 0.0052 - recall: 0.9934 - val_loss: 0.6124 - val_recall: 0.8168
Epoch 80/120
207/207 - 2s - loss: 0.0046 - recall: 0.9949 - val_loss: 0.5232 - val_recall: 0.7148
Epoch 81/120
207/207 - 2s - loss: 0.0051 - recall: 0.9942 - val_loss: 0.6359 - val_recall: 0.8387
Epoch 82/120
207/207 - 2s - loss: 0.0089 - recall: 0.9911 - val_loss: 0.5299 - val_recall: 0.8168
Epoch 83/120
207/207 - 2s - loss: 0.0040 - recall: 0.9957 - val_loss: 0.5856 - val_recall: 0.6490
Epoch 84/120
207/207 - 2s - loss: 0.0031 - recall: 0.9971 - val_loss: 0.6000 - val_recall: 0.8632
Epoch 85/120
207/207 - 2s - loss: 0.0041 - recall: 0.9955 - val_loss: 0.5545 - val_recall: 0.6929
Epoch 86/120
207/207 - 2s - loss: 0.0229 - recall: 0.9776 - val_loss: 0.4691 - val_recall: 0.7355
Epoch 87/120
207/207 - 2s - loss: 0.0035 - recall: 0.9971 - val_loss: 0.5092 - val_recall: 0.7935
Epoch 88/120
207/207 - 2s - loss: 0.0022 - recall: 0.9985 - val_loss: 0.5751 - val_recall: 0.7252
Epoch 89/120
207/207 - 2s - loss: 0.0025 - recall: 0.9975 - val_loss: 0.6065 - val_recall: 0.7213
Epoch 90/120
207/207 - 2s - loss: 0.0049 - recall: 0.9952 - val_loss: 0.5273 - val_recall: 0.8374
Epoch 91/120
207/207 - 2s - loss: 0.0039 - recall: 0.9963 - val_loss: 0.5783 - val_recall: 0.8206
Epoch 92/120
207/207 - 2s - loss: 0.0039 - recall: 0.9956 - val_loss: 0.5681 - val_recall: 0.7019
Epoch 93/120
207/207 - 2s - loss: 0.0036 - recall: 0.9971 - val_loss: 0.7081 - val_recall: 0.8181
Epoch 94/120
207/207 - 2s - loss: 0.0060 - recall: 0.9940 - val_loss: 0.5942 - val_recall: 0.7432
Epoch 95/120
207/207 - 2s - loss: 0.0026 - recall: 0.9977 - val_loss: 0.7486 - val_recall: 0.5781
Epoch 96/120
207/207 - 2s - loss: 0.0327 - recall: 0.9712 - val_loss: 0.4295 - val_recall: 0.7316
Epoch 97/120
207/207 - 2s - loss: 0.0030 - recall: 0.9978 - val_loss: 0.4998 - val_recall: 0.7355
Epoch 98/120
207/207 - 2s - loss: 0.0020 - recall: 0.9982 - val_loss: 0.5508 - val_recall: 0.7394
Epoch 99/120
207/207 - 2s - loss: 0.0012 - recall: 0.9990 - val_loss: 0.5676 - val_recall: 0.7394
Epoch 100/120
207/207 - 2s - loss: 0.0023 - recall: 0.9981 - val_loss: 0.6037 - val_recall: 0.7987
Epoch 101/120
207/207 - 2s - loss: 0.0029 - recall: 0.9978 - val_loss: 0.5457 - val_recall: 0.6787
Epoch 102/120
207/207 - 2s - loss: 0.0038 - recall: 0.9964 - val_loss: 0.6129 - val_recall: 0.7510
Epoch 103/120
207/207 - 2s - loss: 0.0065 - recall: 0.9942 - val_loss: 0.4332 - val_recall: 0.7148
Epoch 104/120
207/207 - 2s - loss: 0.0036 - recall: 0.9970 - val_loss: 0.5503 - val_recall: 0.7252
Epoch 105/120
207/207 - 2s - loss: 0.0053 - recall: 0.9940 - val_loss: 0.5807 - val_recall: 0.8813
Epoch 106/120
207/207 - 2s - loss: 0.0034 - recall: 0.9966 - val_loss: 0.5515 - val_recall: 0.8077
Epoch 107/120
207/207 - 2s - loss: 0.0026 - recall: 0.9973 - val_loss: 0.6207 - val_recall: 0.7561
Epoch 108/120
207/207 - 2s - loss: 0.0022 - recall: 0.9979 - val_loss: 0.5688 - val_recall: 0.8232
Epoch 109/120
207/207 - 2s - loss: 0.0029 - recall: 0.9973 - val_loss: 0.6706 - val_recall: 0.6942
Epoch 110/120
207/207 - 2s - loss: 0.0046 - recall: 0.9955 - val_loss: 0.5698 - val_recall: 0.6168
Epoch 111/120
207/207 - 2s - loss: 0.0150 - recall: 0.9870 - val_loss: 0.5057 - val_recall: 0.7239
Epoch 112/120
207/207 - 2s - loss: 0.0017 - recall: 0.9984 - val_loss: 0.5736 - val_recall: 0.7406
Epoch 113/120
207/207 - 2s - loss: 0.0011 - recall: 0.9993 - val_loss: 0.6626 - val_recall: 0.7032
Epoch 114/120
207/207 - 2s - loss: 0.0024 - recall: 0.9979 - val_loss: 0.5803 - val_recall: 0.7161
Epoch 115/120
207/207 - 2s - loss: 0.0015 - recall: 0.9992 - val_loss: 0.5583 - val_recall: 0.7045
Epoch 116/120
207/207 - 2s - loss: 0.0032 - recall: 0.9968 - val_loss: 0.5617 - val_recall: 0.7626
Epoch 117/120
207/207 - 2s - loss: 0.0039 - recall: 0.9968 - val_loss: 0.5976 - val_recall: 0.7394
Epoch 118/120
207/207 - 2s - loss: 0.0096 - recall: 0.9905 - val_loss: 0.4794 - val_recall: 0.7923
Epoch 119/120
207/207 - 2s - loss: 0.0016 - recall: 0.9982 - val_loss: 0.6251 - val_recall: 0.7716
Epoch 120/120
207/207 - 2s - loss: 0.0020 - recall: 0.9984 - val_loss: 0.6338 - val_recall: 0.7561
dict_keys(['loss', 'recall', 'val_loss', 'val_recall'])
Wall time: 3min 23s
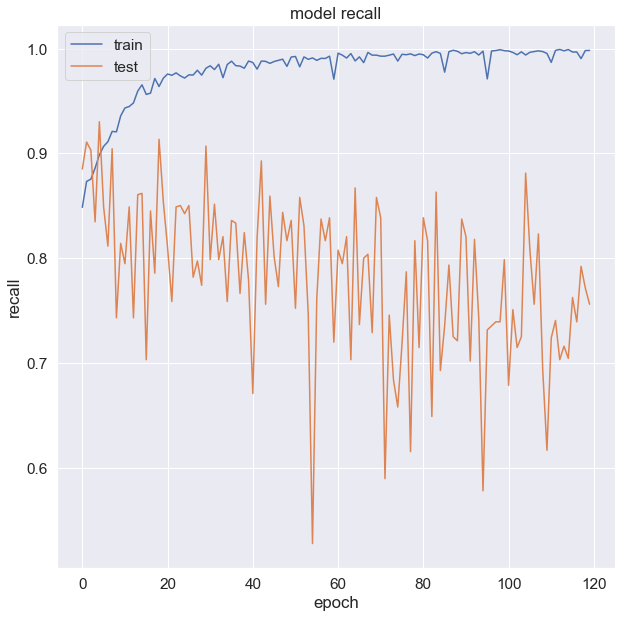
# summarize history for Accuracy
fig_acc = plt.figure(figsize=(10, 10))
plt.plot(history.history['recall'])
plt.plot(history.history['val_recall'])
plt.title('model recall')
plt.ylabel('recall')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
fig_acc.savefig("model_recall.png")
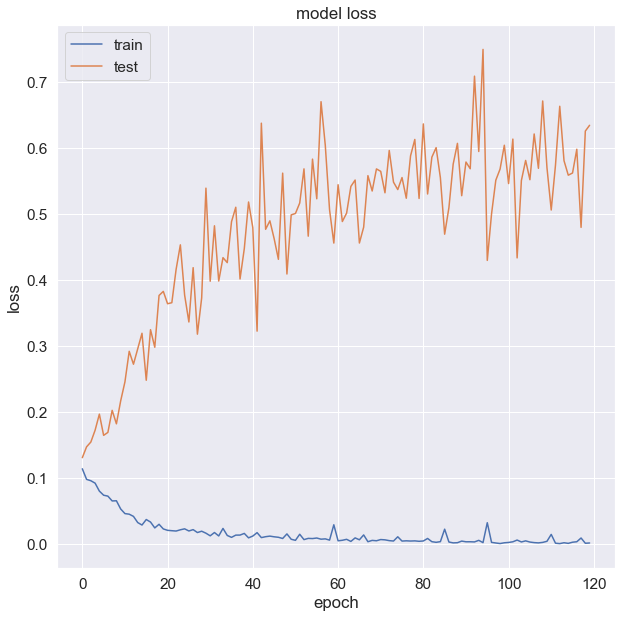
# summarize history for Loss
fig_acc = plt.figure(figsize=(10, 10))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
fig_acc.savefig("model_loss.png")
# training metrics
scores = model.evaluate(seq_array, label_array, verbose=1, batch_size=200)
print('Accurracy: {}'.format(scores[1]))
230/230 [==============================] - 1s 4ms/step - loss: 0.0657 - recall: 0.9741
Accurracy: 0.9740694761276245
# preds
y_pred = (model.predict(seq_array) > 0.5).astype("int32")
y_true = label_array
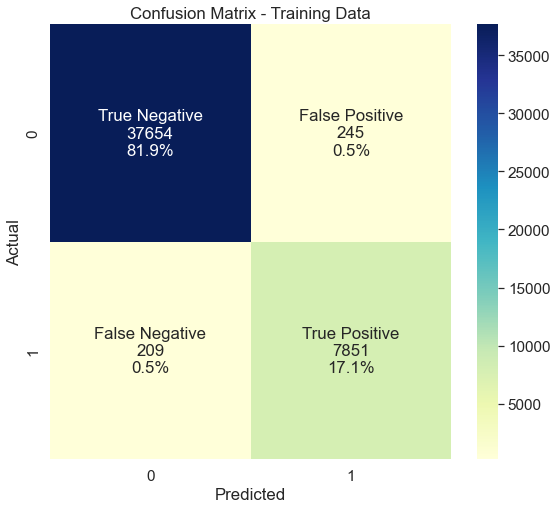
# Confusion matrix
cm = confusion_matrix(y_true, y_pred)
plt.figure(figsize=(9,8))
classes = ["True Negative","False Positive","False Negative","True Positive"]
values = ["{0:0.0f}".format(x) for x in cm.flatten()]
percentages = ["{0:.1%}".format(x) for x in cm.flatten()/np.sum(cm)]
combined = [f"{i}\n{j}\n{k}" for i, j, k in zip(classes, values, percentages)]
combined = np.asarray(combined).reshape(2,2)
sns.set(font_scale=1.4)
b = sns.heatmap(pd.DataFrame(cm, range(2), range(2)), annot=combined, fmt="", cmap='YlGnBu')
b.set(title='Confusion Matrix - Training Data')
b.set(xlabel='Predicted', ylabel='Actual')
plt.show()
# compute precision and recall
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
print( 'precision = ', precision, '\n', 'recall = ', recall)
precision = 0.9697381422924901
recall = 0.9740694789081886
Evaluate model on test data
consists of many right censored engines that are in use for a random number of cycles with a full cycle history starting from one but not necessarily have seen failure yet [RUL > 0] (real life scenario)
seq_array_test_last = [test_df[test_df['id']==id][scols].values[-window_width:]
for id in test_df['id'].unique() if len(test_df[test_df['id']==id]) >= window_width]
seq_array_test_last = np.asarray(seq_array_test_last).astype(np.float32)
machine_mask = [len(test_df[test_df['id']==id]) >= window_width for id in test_df['id'].unique()]
label_array_test_last = test_df.groupby('id')['label1'].last()[machine_mask] #.values
# if best iteration's model was saved then load and use it
if os.path.isfile(model_path):
estimator = tf.keras.models.load_model(model_path)
# test metrics
scores_test = estimator.evaluate(seq_array_test_last, label_array_test_last, verbose=2)
# make predictions and compute confusion matrix
y_pred_test = (estimator.predict(seq_array_test_last) > 0.5).astype("int32")
y_true_test = label_array_test_last
test_set = pd.DataFrame(y_pred_test)
test_set.to_csv('binary_submit_test.csv', index = None)
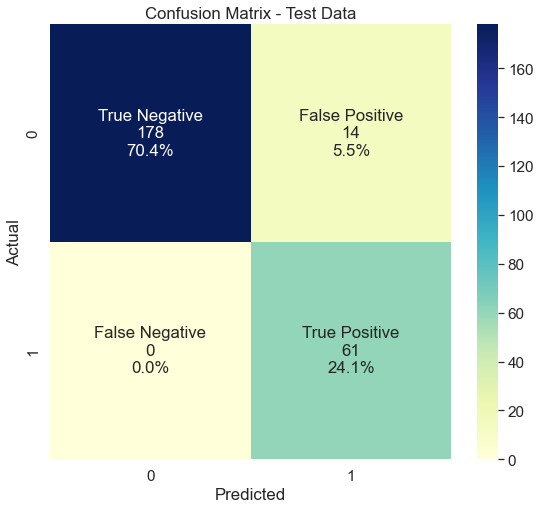
# Confusion matrix
cm = confusion_matrix(y_true_test, y_pred_test)
plt.figure(figsize=(9,8))
sns.set(font_scale=1.4)
classes = ["True Negative","False Positive","False Negative","True Positive"]
values = ["{0:0.0f}".format(x) for x in cm.flatten()]
percentages = ["{0:.1%}".format(x) for x in cm.flatten()/np.sum(cm)]
combined = [f"{i}\n{j}\n{k}" for i, j, k in zip(classes, values, percentages)]
combined = np.asarray(combined).reshape(2,2)
b = sns.heatmap(pd.DataFrame(cm, range(2), range(2)), annot=combined, fmt="", cmap='YlGnBu')
b.set(title='Confusion Matrix - Test Data')
b.set(xlabel='Predicted', ylabel='Actual')
plt.show()
# compute precision and recall
precision_test = precision_score(y_true_test, y_pred_test)
recall_test = recall_score(y_true_test, y_pred_test)
#f1_test = 2 * (precision_test * recall_test) / (precision_test + recall_test)
f1_test = f1_score(y_true_test, y_pred_test)
print( 'Precision: ', precision_test, '\n', 'Recall: ', recall_test,'\n', 'F1-score:', f1_test )
8/8 - 1s - loss: 0.1839 - recall: 1.0000
Precision: 0.8133333333333334
Recall: 1.0
F1-score: 0.8970588235294117
# Plot in red color the predicted labels and in green color the
# actual label to inspect visually that the model succeeds in correct classification.
plt.figure( figsize=(16, 3) )
# look at partial array for better visualization
sta = 215
sto = 240
# actual label
plt.scatter(y_true_test.index[sta:sto], y_true_test[sta:sto], color="green", s=160)
# predicted label
plt.scatter(y_true_test.index[sta:sto], y_pred_test[sta:sto], color="red", s=35)
plt.title('actual vs. prediction for a slice of machine ids')
plt.ylabel('failure imminent 1=true / 0=false')
plt.xlabel('machine id')
plt.legend(['actual label', 'predicted label' ], loc='center left')
plt.show()
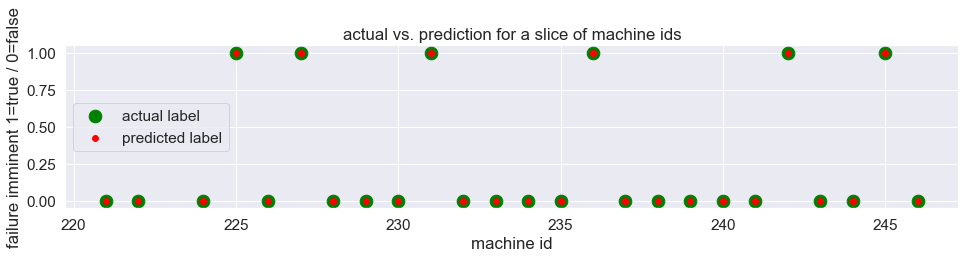
Including the Survival Analysis in my blog earlier, we have come quite some way in working with this data set and here is the result with a pretty reliable model.
Implemented here as Gated Recurrent Units, this really shows the power of Recurrent Neural Networks, which may be further improved with more data and measurements. False Negatives are successfully avoided at all with the test data, although this is also favored due to the low amount of engines within that set and thus has low statistical power. For this reason I waive to translate this Classification Screening to a Process Sigma metric that describes the number of ‘defects’ (in this context number of False Negative Classifications) per million opportunities.
In any way such a model is certainly only a starting point in the search for model that can be used in production with its specific goals that may be given/set.